Sciences
Age of the Universe
How old is the universe? This question concerns not only cosmologists but also individuals interested in natural phenomena. Within the framework of the cosmological model, the Friedmann-Lemaître equations, derived from Einstein's field equations for a homogeneous and isotropic universe, describe the development of the cosmos. From these, one obtains the following equation for the age of the universe: \[t(R) = \frac{1}{H_0} \int_{0}^{R} \frac{dR}{\sqrt{\Omega_m R^{-1} + (1-\Omega_m-\Omega_{\Lambda})+\Omega_{\Lambda} R^2}} \tag{1}\] In this, $t(R)$ denotes the age of the universe, $H_0$ the current Hubble parameter, and $\Omega_m$ and $\Omega_{\Lambda}$ the dimensionless density parameters of matter and the vacuum. R(t) is the scale factor. The following relationship can be defined as: \[\frac{R(t_0)}{R(t)}=z+1=\frac{\lambda_0}{\lambda_e}-1 \tag{2}\] which indicates the size ratio of the present universe to the universe at time t.If the scale factor R(t0), which corresponds to the present size of the universe, is set to 1, then equation (2) simplifies to the well-known equation \[R(t)=\frac{1}{z+1} \tag{3} \] Depending on the choice of parameters $\Omega_m$ and $\Omega_{\Lambda}$ in equation (1), one deals with different types of universes. The simplest, yet hypothetical case is a completely empty universe, which contains neither mass nor vacuum energy. In this cosmos, the parameters $\Omega_m$ and $\Omega_{\Lambda}$ are equal to zero, and equation (1) simplifies to \[t(R)=\frac{1}{H_0}\int_{0}^{R} dR \tag{4} \] The integration yields \[t(R)=\frac{1}{H_0}\cdot R \tag{5} \] Setting $t(R) = t0$ in (eq. 5) makes the scale factor R equal to 1, and obtains \[t_0=\frac{1}{H_0} \tag{6} \] In other words, the age of an empty universe with Ωm and ΩΛ equal to zero is equal to the reciprocal of the Hubble parameter. This time is also referred to as the Hubble time. With the current Hubble parameter $H_0 = 67.8\,\mathrm{km/s/Mpc}$, $t_0$ equals 14.48 billion years. As equation (5) shows, this universe expands forever proportional to time t. In 1932, Einstein and DeSitter proposed a matter cosmos with $\Omega_m = 1$ and $\Omega_{\Lambda} = 0$. In this universe, the total density is equal to the critical density, and therefore the curvature k is zero. At that time, it was believed that this so-called Einstein-DeSitter cosmos corresponds to the universe in which we live. The Einstein-DeSitter cosmos is also of cosmological interest because it marks the boundary between an open universe (curvature k < 1) and a closed universe (curvature k > 1), that is, between a universe that expands forever and one that, after a period of expansion, collapses back into itself. For the Einstein-DeSitter cosmos, equation (1) reads \[t(R) = \frac{1}{H_0} \int_{0}^{R} \sqrt{R} \, dR \tag{7}\] The integration yields \[t(R) = \frac{2}{3}\frac{1}{H_0}\sqrt{R^3} \tag{8}\] setting $t(R) = t_0$ again and thus the scale factor $R = 1$, it obtains \[t(R) = \frac{2}{3}\frac{1}{H_0} \tag{9}\] Conclusion: The age of the matter-dominated Einstein-DeSitter cosmos is equal to 2/3 of the Hubble time. This time, i.e., the time from the beginning of the cosmos to the present day, is also referred to as the Friedmann time. This applies not only to the Einstein-DeSitter cosmos but to all universes that start with a Big Bang. With $H_0 = 67.8\,\mathrm{km/s/Mpc}$, the Friedmann time of the Einstein-DeSitter cosmos is 9.65 billion years. Based on current knowledge, it is now assumed that the universe has $\Omega_{m} = 0.317$ and $\Omega_{\Lambda} = 0.683$. With these values, equation (1) can only be solved numerically. As a result, one obtains an age $t_0$ of approximately 13.8 billion years. Instead of equation (1), the approximate formula (10), which is valid in the range $0.1 ≤ \Omega_{m} ≤ 1$ and $\Omega_{\Lambda} ≤ 1$, also provides a value for t0 accurate to within a few percent. \[t(R) = \frac{2}{3}\frac{1}{H_0}(0.7\,\Omega_{m} + 0.3 - 0.3\,\Omega_{\Lambda}) \tag{10}\] Considering the temporal development of this universe, it is noticeable that it initially expands decelerating until about 8 billion years after its formation, and then it expands acceleratingly. Measurements of the brightness of highly redshifted Type Ia supernovae have confirmed this result. The following graph shows the temporal development of the discussed universes plus a universe with $\Omega_{m} = 0.3$ and $\Omega_{\Lambda} = 0$. On the X-axis, time is plotted in billions of years into the past (negative sign), and on the Y-axis, the relative size of the universe. The time t = 0 corresponds to the present, and $R(t)/R_0 = 1$ corresponds to the current size of the cosmos. From the graph, the age of the universe can be directly read off depending on the scale factor. The Friedmann time is marked for the Einstein-DeSitter cosmos.
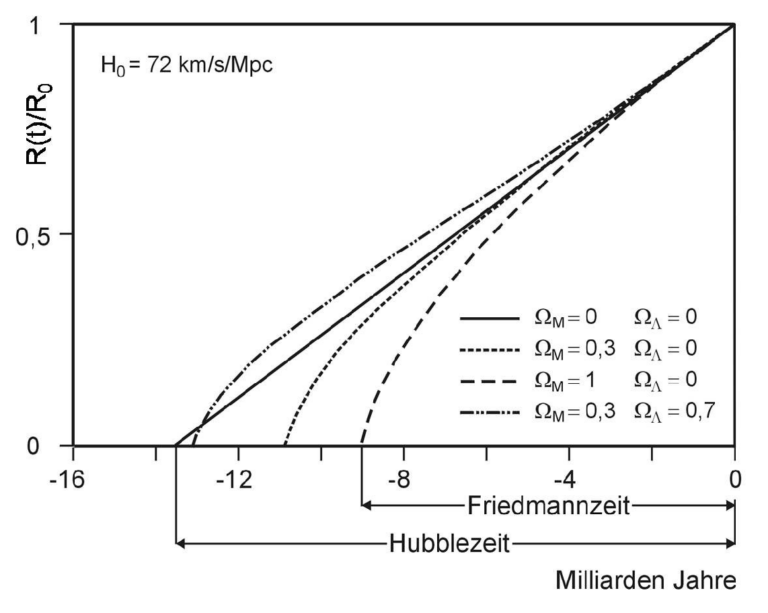
Attentive readers will have noticed that, as noted in the top left of the graph, the calculations were carried out with a Hubble parameter $H_0 = 72\,\mathrm{km/s/Mpc}$. With the current Hubble parameter $H_0 = 67.8\,\mathrm{km/s/Mpc}$, the foot points of the expansion curves shift slightly to the left, although the course and shape of the curves remain unchanged. How does the Friedmann time $t_0$ of our universe ($\Omega_{m} = 0.317$ and $\Omega_{\Lambda} = 0.683$) match the observations? A first clue is provided by the approximately 150 known globular clusters in our galaxy. Their typical age of 12.7 billion years fits the theoretical value. The oldest galaxies discovered so far come closer to the calculated age. The galaxy UDFy-38135539 with a redshift of $z = 8.6$ is nearly 13.3 billion years old. The galaxy EGS8p7, with $z = 8.68$, is eight million years older. Finally, let us consider the cosmic background radiation that originated shortly after the Big Bang. With a redshift of $z \cong 1100$, it is only 380,000 years younger than the calculated Friedmann time $t_0$. Thus, the calculation and observation agree sufficiently well.
